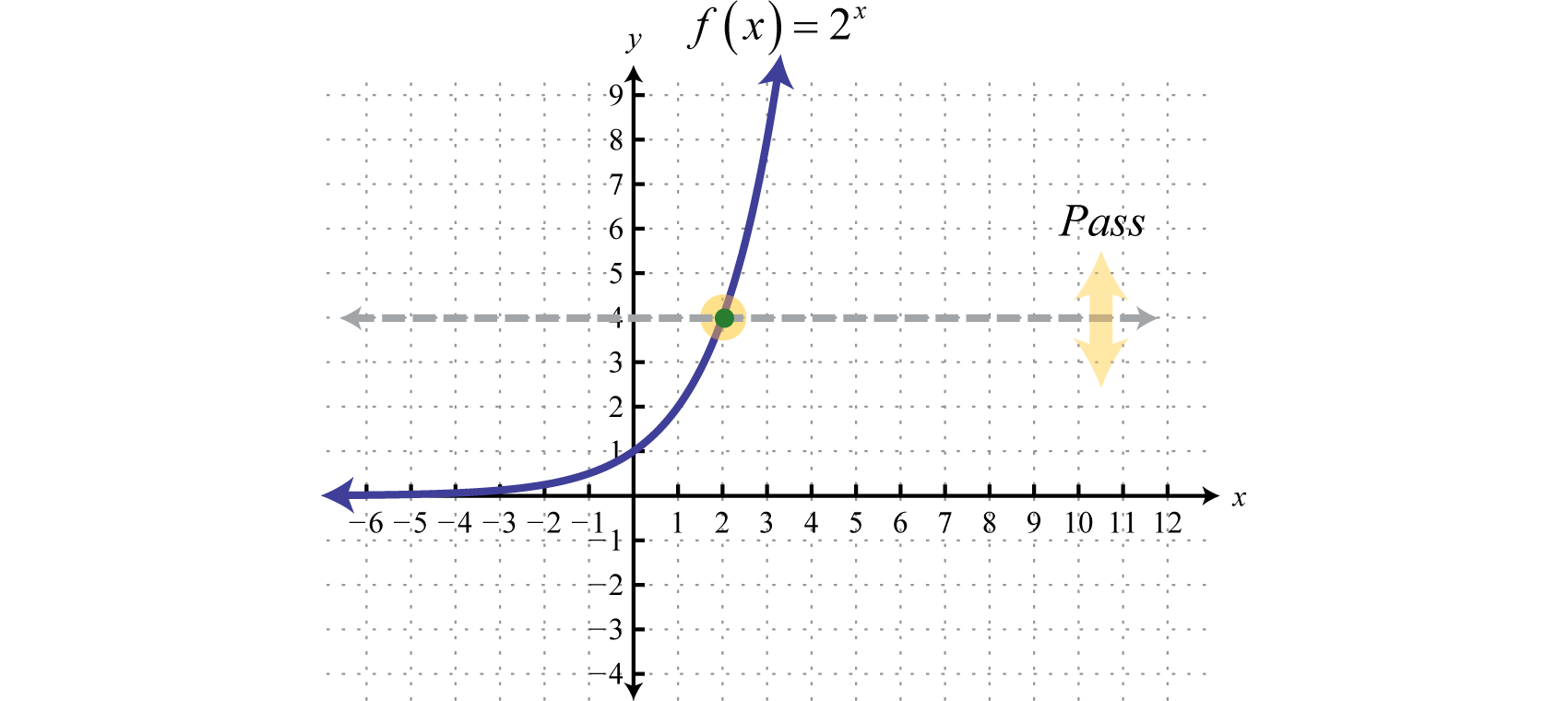
You can see this behavior in any basic exponential function, so we'll use y = 2 x as representative of the entire class of functions On the lefthand side of the x axis, the graph5/21/16 · Explanation You can choose "easy" values for x remembering that it will be a typical exponential but shifted up of 1 unit we can choose values such as −2, − 1,0,1,2 for x and get;Graphing the Natural Exponential Function y = e^x Easy Study Hack
Introduction To Exponential Functions
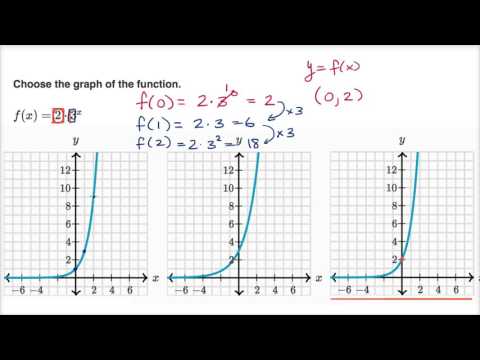
Graph the exponential function y=5(2)^x
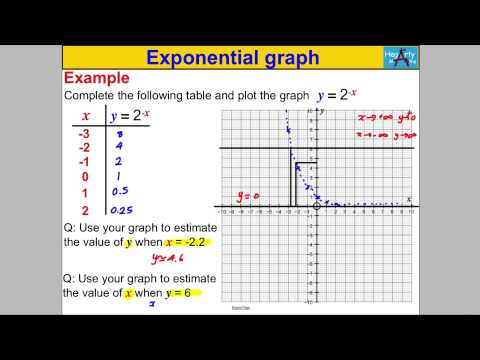
Graph the exponential function y=5(2)^x-Graph the function using a table of values Define the domain and range Simple y = 2 x Advanced y=(2 x)180 seconds Q Suppose a culture of bacteria begins with 5000 cells and dies by 30% each year Write an equation that represents this situation answer choices y=5000 (07) x y=30 (5000) x y=5000 (13) x y=5000x x s



What Is An Exponential Function Math Class 21 Video Study Com
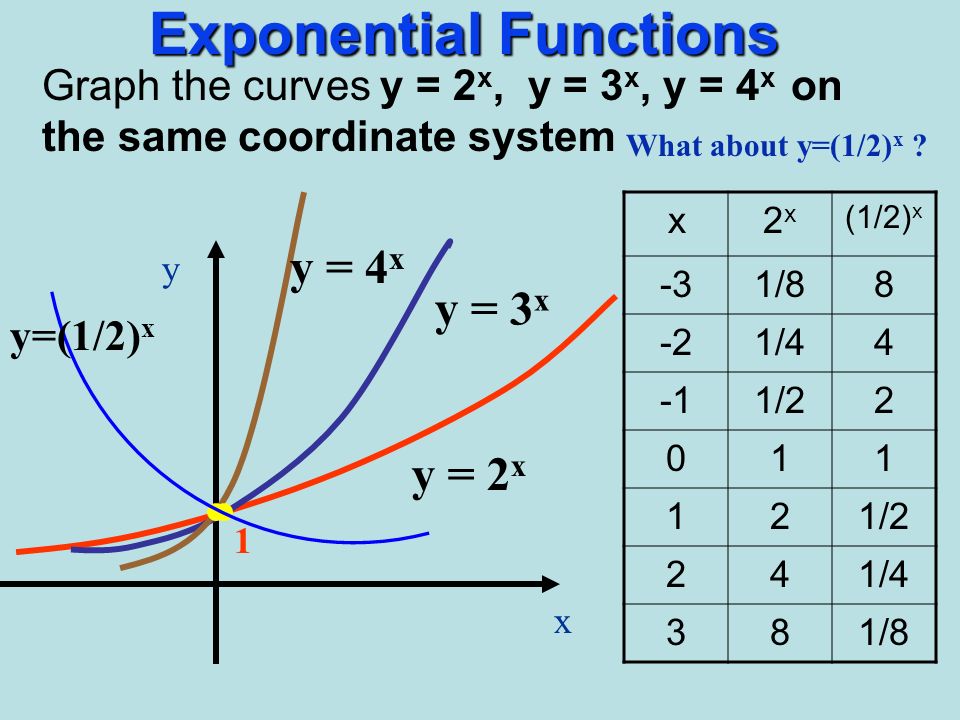
Y = 2 x This is a basic exponential function y = 2x (is same as y = 05 x) The (x) exponent makes a reflection in the yaxis y = 2 x The negative sign makes each value negative and gives a reflection in the xaxis Example 2 y = 10 x The bigger the base number the steeper the graph y = 10 x2 The graph is moved 2 units forward y = 10 x − 2Notice that the graph has the x axis as an asymptote on the left, and increases very fast on the right Changing the base changes the shape of the graph Replacing x with − x reflects the graph across the y axis;Free graphing calculator instantly graphs your math problems Mathway Visit Mathway on the web Download free on Google Play Download free on iTunes Download free on Amazon Download free in Windows Store get Go Graphing Basic Math PreAlgebra Algebra Trigonometry Precalculus Calculus Statistics Finite Math Linear Algebra
We are given the exponential function {eq}y=2(2^x) {/eq} Graphing this function and comparing this to the graph of {eq}y=2^x {/eq}, we have Solution The parent function is {eq}y=2^x {/eq}The domain of f(x) = 2x is all real numbers, the range is (0, ∞), and the horizontal asymptote is y = 0 To get a sense of the behavior of exponential decay, we can create a table of values for a function of the form f(x) = bx whose base is between zero and one We'll use the function g(x) =Exponential Functions Topics 1 Solving exponential equations using exponent rules 2 Graphing exponential functions 3 Graphing transformations of exponential functions 4 Finding an exponential function given its graph 5 Exponential growth and decay by a factor 6 Exponential decay Halflife 7 Exponential growth and decay by
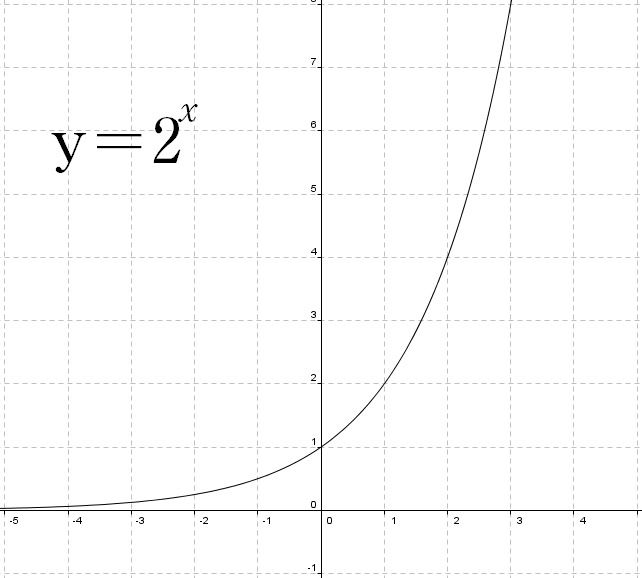
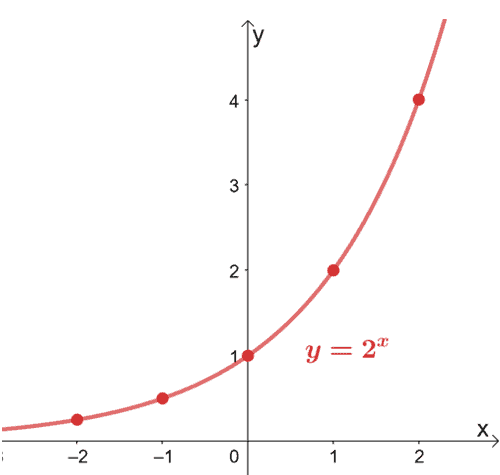
8/5/15 · In an exponential function, the independent variable, or xvalue, is the exponent, while the base is a constant For example, y = 2 x would be an exponential functionAn ordinary exponential function always has the points (0, 1) , ( 1 , base) and (1, 1/base ) since The x axis is an asymptote, the graph never crosses the x –axis When the base is greater than 1 And when the base is smaller than 1 Example To calculate the values of y , raise x to the power of the base y = 2 xAlgebra Graph y=2^x y = 2x y = 2 x Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = 0 y = 0


Exponential Growth Its Properties How Graph Relates To The Equation And Formula Visual Lesson Math Warehouse


Introduction To Exponential Functions
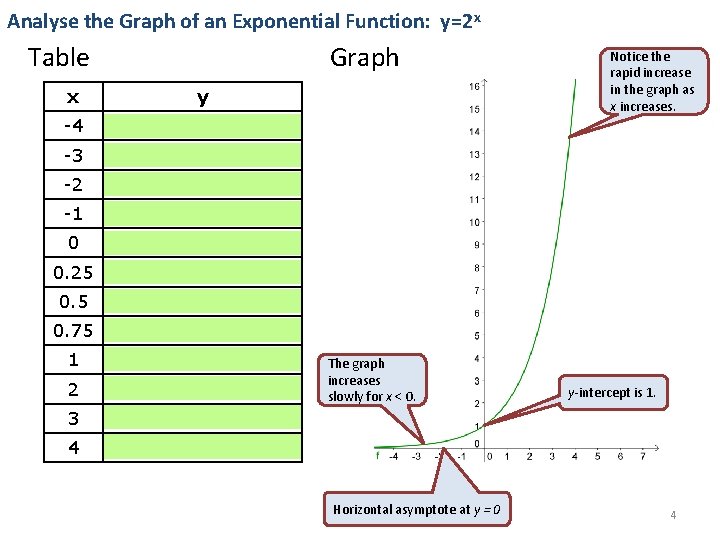
Algebra 1 Unit 4 Exponential Functions Notes 3 Asymptotes An asymptote is a line that an exponential graph gets closer and closer to but never touches or crosses The equation for the line of an asymptote for a function in the form of f(x) = abx is always y = _____ Identify the asymptote of each graphAlgebra 1 Graphs of Exponential Functions 4 Example a) Describe the domain and the range of the function y = 2 x b) Describe the domain and the range of the function y = 3(1/2) x Show Stepbystep SolutionsIn general, the graph of the basic exponential function y = a x drops from ∞ to 0 when 0 < a < 1 as x varies from − ∞ to ∞ and rises from 0 to ∞ when a > 1 The exponential function y = a x , can be shifted k units vertically and h units horizontally with the equation y = a ( x h ) k


Exponential Functions


Graphing Exponential Functions
Graphing Exponential Functions DRAFT 10th 12th grade 0 times Mathematics 0% average accuracy 16 minutes ago aberorange 0 Save Edit Edit What is the domain and range of the function y=2 x ?Use the graph to help!Where a is a constant Figure 1 shows the graph of y=2^{x}, in blue, together with that of its gradient, in redNotice that the function itself and the gradient are very similar to one another they both rise rapidly as x gets larger Figure 1 graph of y=2^{x} (blue line) and its gradient (red line) Figure 2 shows y=3^{x} together with its gradient Again, the two curves are very


Graphing Exponential Functions Using Transformations Youtube



5 2 Exponential Functions Objective Graph And
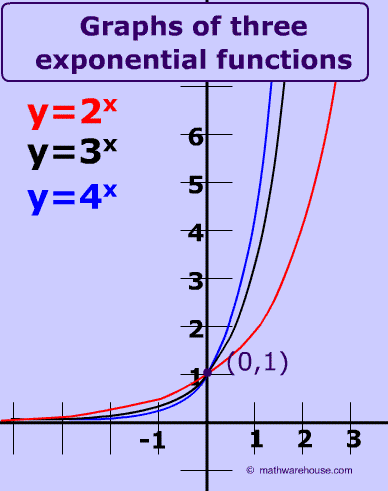
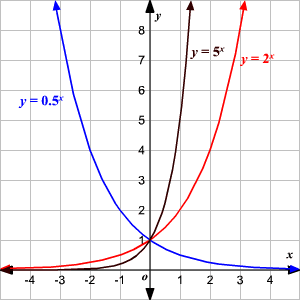
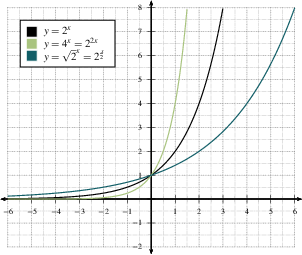
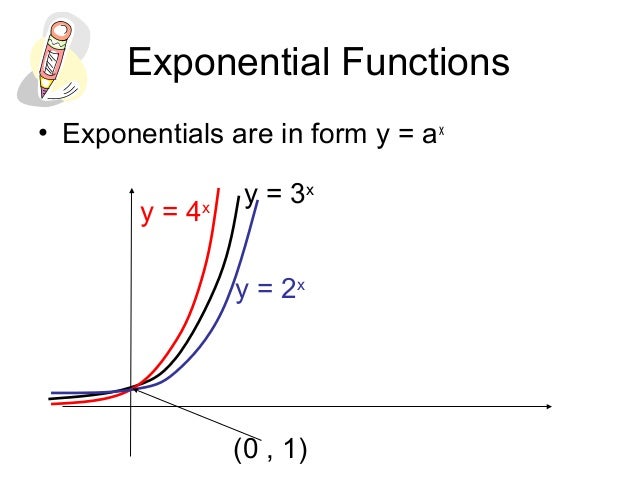
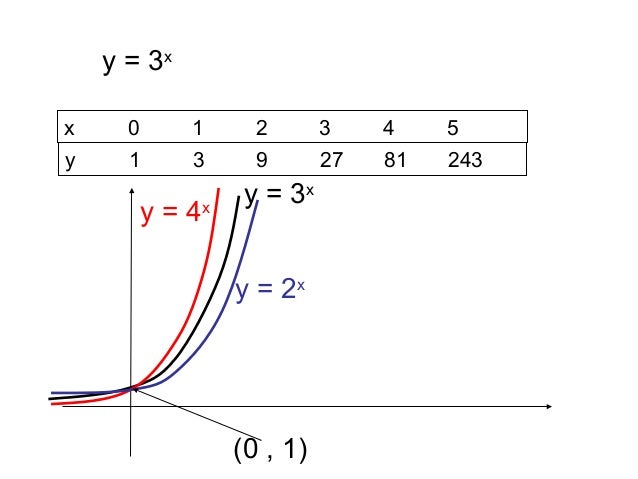
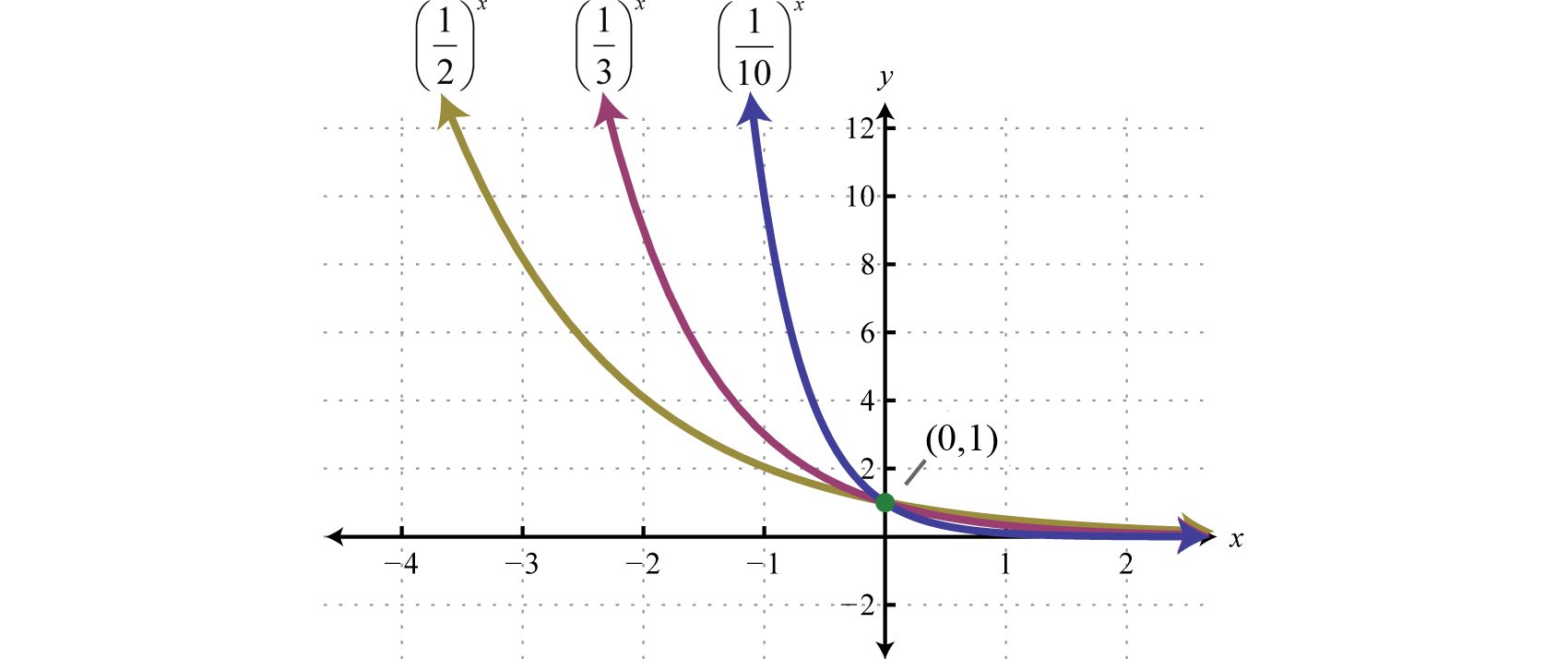
2/13/15 · Press GRAPH to observe the graph of the exponential function along with the line for the specified value of;Graphs of Exponential Functions The graphs of all exponential functions have similar characteristics, as shown in Examples 2, 3, and 5 Graphs of yax In the same coordinate plane, sketch the graph of each function a b Solution The table below lists some values for each function, and Figure 31 shows the graphs of the two functions8/29/17 · The base \(b\) of an exponential function affects the rate at which it grows Below we have graphed \(y = 2^{x} , y = 3^{x}\), and \(y = 10^{x}\) on the same set of axes Figure \(\PageIndex{2}\) Note that all of these exponential functions have the same \(y\)intercept, namely \((0, 1)\)



Let S Learn Exponential Functions And Their Graphs



How To Find Equations For Exponential Functions Studypug
The formula is y= abx when a≠0, b>0, b≠1 it is continuous and "one and one" meaning it has to beFor example, graph $2^{x3}$ and $2^{x1}$ and $2^x$ and $2^x5$, etc You will need this practice for the questions that come later in this learning module You may need to refer to some precalculus material to recall how to do such transformations11/26/16 · When graphing an exponential function, remember that the graph of an exponential function whose base number is greater than 1 always increases (orrises) as it moves to the right;


Graphing Exponential Functions


Exploring Exponential Functions
Graph each exponential function $$ y=2^{x}3 $$ Answer View Answer Topics No Related Subtopics Algebra A Combined Function 4th Chapter 12 Exponential and Logarithmic Functions Section 3 Exponential Functions Discussion You must be signed in to discuss Top Educators Recommended VideosThe exponential graph of a function represents the exponential function properties Let us consider the exponential function, y=2 x The graph of function y=2 x is shown below First, the property of the exponential function graph when the base is greater than 1 Exponential Function Graph for y=2 x The graph passes through the point (0,1)There is no value of x that will make 3 x equal 0 or a negative number, a property of all exponential math functions Comparing the Graph of y = 3 x and y = 10 x The graph of a base that is greater than 1 has positive slope, a base less than 1 has negative slope, another property of all exponential functions



How To Find Equations For Exponential Functions Studypug



How To Find Equations For Exponential Functions Studypug
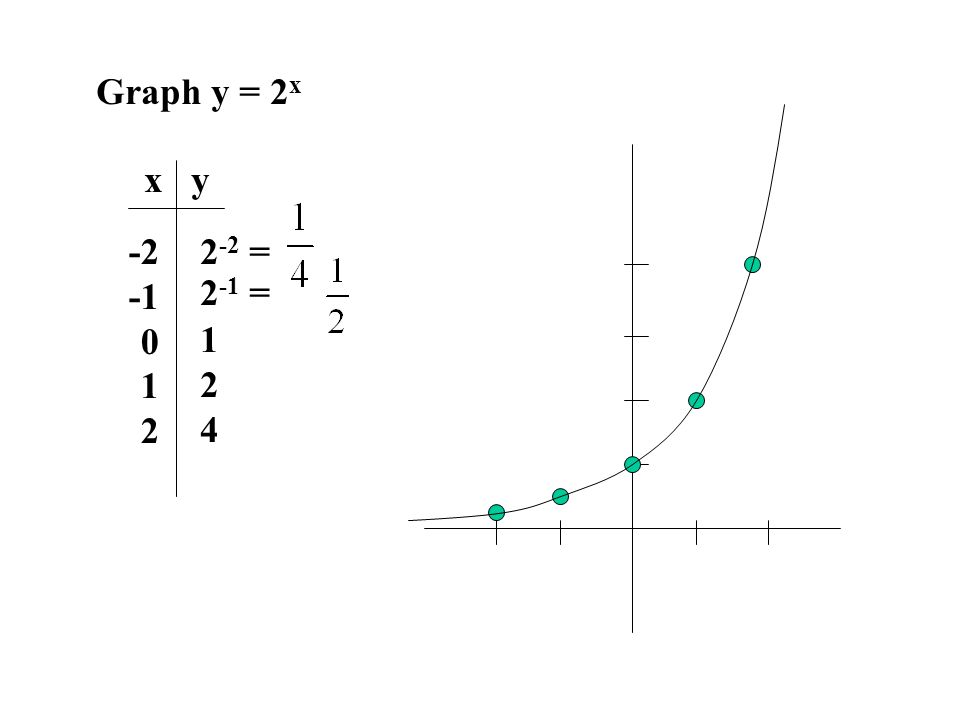
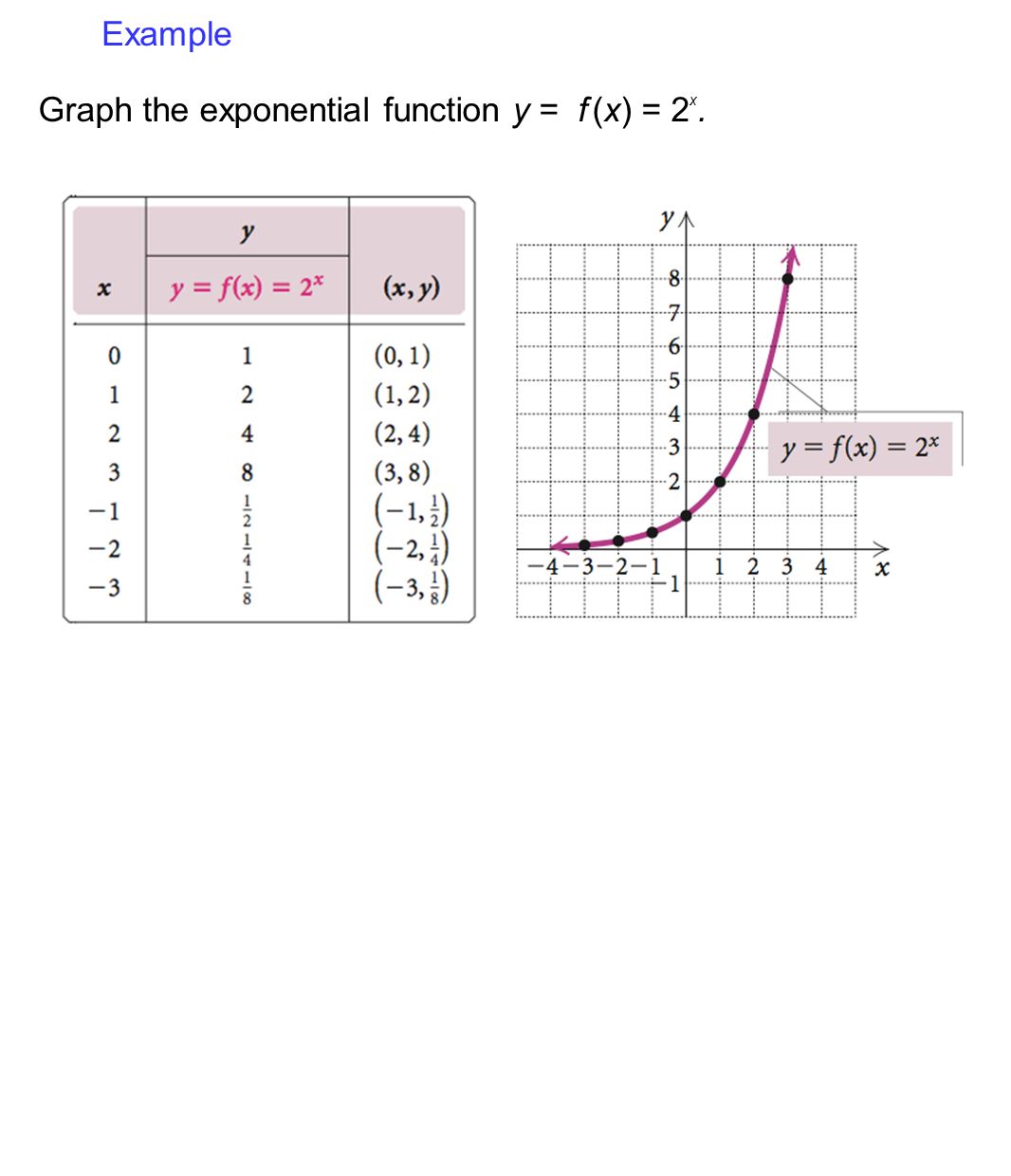
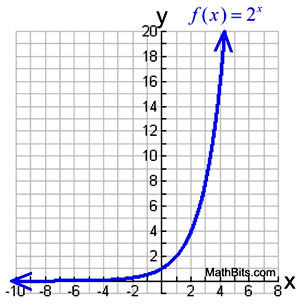
Graphing Exponential Functionsksia2 Author Mike Created Date 9/5/12 AMGraph an Exponential Function y=2x x Y=2x 3 23=1/8 2 22=1/4 1 21=1/2 0 =1 1 21=2 2 22=4 3 23=8 Domain all real #s Range all positive #s What is an Exponential Function?Given an exponential function of the form f (x) = b x, f (x) = b x, graph the function Create a table of points Plot at least 3 3 point from the table, including the y intercept ( 0 , 1 )



Exponential Functions Ck 12 Foundation
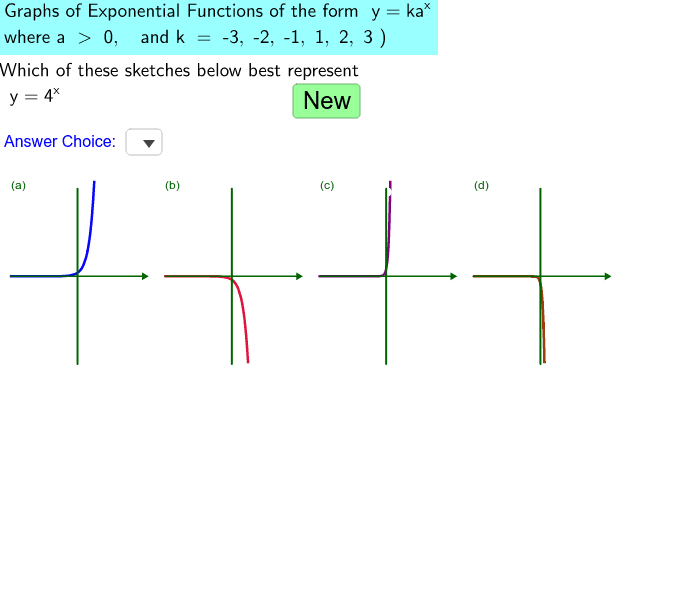


Self Assessment Graphs Of Exponential Functions Y K A X Geogebra
The exponential function equation to this graph is y = 2 x y=2^x y = 2x, and is the most simple exponential graph we can make If you're wondering what y = 1 x y=1^x y = 1x would look like, here's its exponential graph Graph of y = 1^x Now, as to the reason why the graphs of y = 2 xExample 1 Sketch the graph and determine the domain and range f (x) = 10 x 5 Solution The base 10 is used often, most notably with scientific notation Hence, 10 is called the common baseIn fact, the exponential function y = 10 x is so important that you will find a button 10 x dedicated to it on most modern scientific calculators In this example, we will sketch the basic graph y = 10The graphs of exponential decay functions can be transformed in the same manner as those of exponential growth Example 5 Graph the following function State the domain and range y = (1/3) x Solution Make a table of values Then plot the points and sketch the graph



Timed 30pts The Graphs Of The Quadratic Function Y 2x 2 And The Exponential Function Y 2 X Are Brainly Com


Bestmaths
Answer choices Domain All Real Numbers Range y>0We're asked to graph y is equal to 5 to the X power and we'll just do this the most basic way we'll just try out some values for X and see what we get for y and then we'll plot those coordinates so let's try some negative and some positive values and I'll try to Center them around 0 so this will be my X values this will be my Y values let's start first with something reasonably negative but notThen the graph is So y = ( 1 / 3 ) –x does indeed model growth For the record, however, the base for exponential functions is usually greater than 1, so growth is usually in the form " 3 x " (that is, with a "positive" exponent) and decay is usually in the form " 3 –x " (that is, with a "negative" exponent)



Transformation Of Exponential Functions Examples Summary Math Class 21 Video Study Com
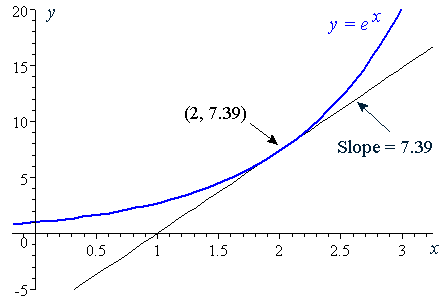


6 Derivative Of The Exponential Function
1/2/21 · Graphing Exponential Functions Before we begin graphing, it is helpful to review the behavior of exponential growth Recall the table of values for a function of the form \(f(x)=b^x\) whose base is greater than one We'll use the function \(f(x)=2^x\)So, if we were to graph y=2x, the graph would be a reflection about the yaxis of y=2 x and the function would be equivalent to y=(1/2) x The graph of y=2x is shown to the right Properties of exponential function and its graph when the base is between 0 and 1 are given The graph passes through the point (0,1) The domain is all real numbersTo find the value of we compute the point of intersection Press 2ND then CALC Select "intersect" and press ENTER three times The point of intersection gives the value of x for the indicated value of the function
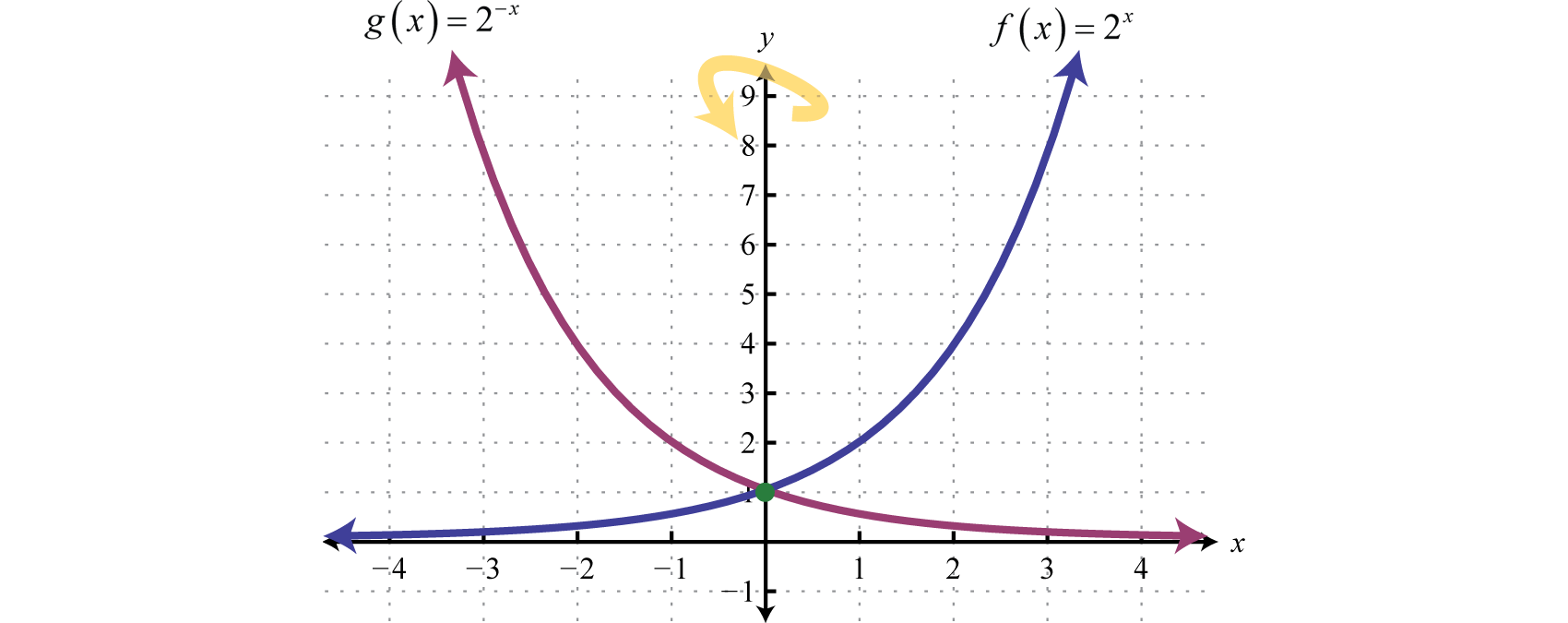


Exponential Functions And Their Graphs


Exponential Functions Functions
As the graph moves to the left, it always approaches 0 but never actually get there For example, f(x) = 2 x is an exponential function, as is3/26/18 · If the equation was #y=2^(x)# y would be in exponential decay, with #y# approaching 0 as #x# goes to infinity Again, we can show this on a plot (see below) graph{2^(x) 2317, 56, 6, 3312} Basically, the sign of the exponent tells you if the functionExponential Functions and Graphs \n \n Draw the graphs of y = 2 x y = 2 x and y = (1 2) x y = (1 2) x on the same set of axes\n Is the x xaxis and asymptote or and axis of symmetry to both graphs ?
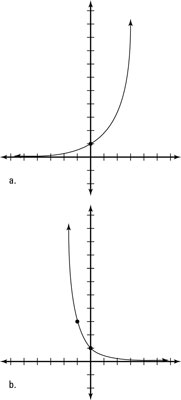


How To Graph And Transform An Exponential Function Dummies
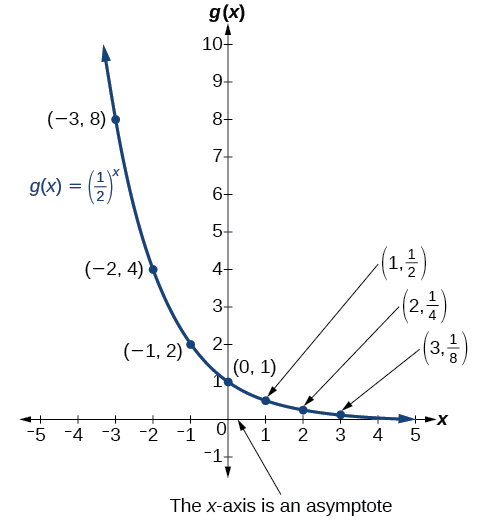


Graphs Of Exponential Functions Algebra And Trigonometry
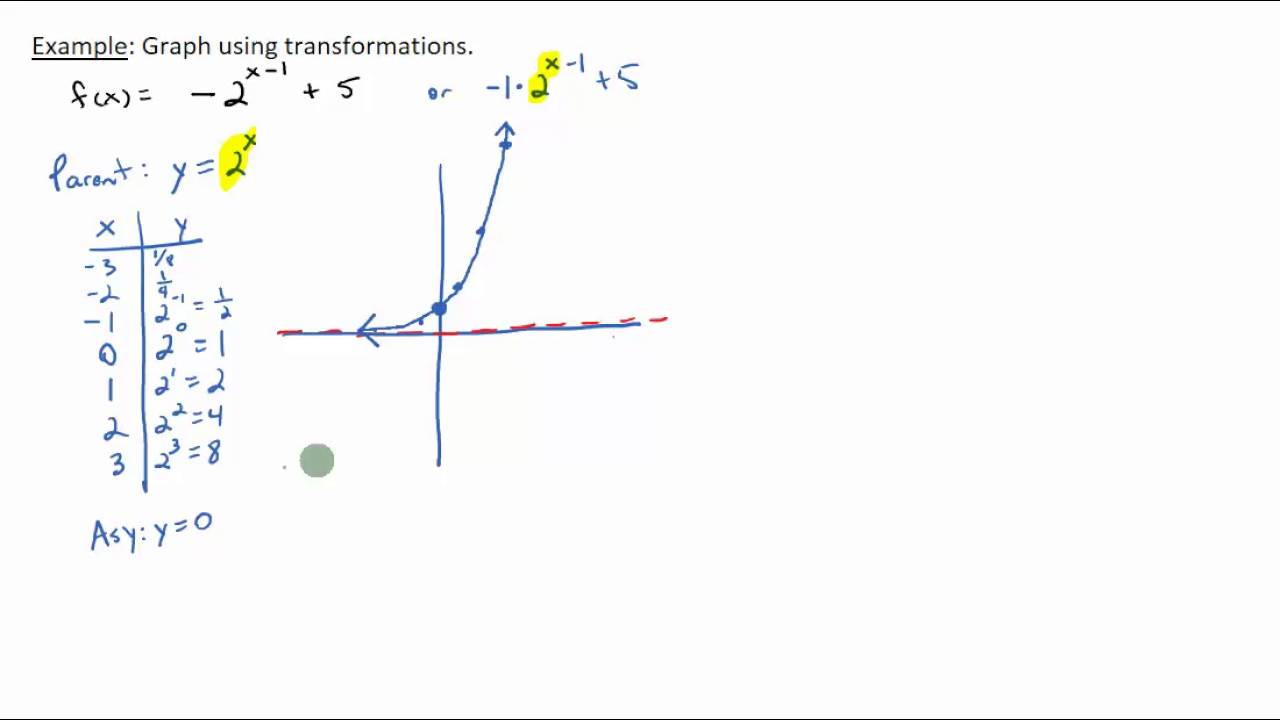
Section 92 Exponential Functions and Their Graphs The functions \(y=2^x\) and \(y=7 \cdot 2^x\) are both shown in Figure 9216 Three pairs of points have been highlighted to show the attendant leftward shift of a little less than 3 units{'transcript' "Okay, So this problem wants us to graft the function y equals negative or to the X power Um, so for this problem, we deceive an X Y access I'm drawing my XX is higher because because it's negative, it's gonna be beneath the X axisSal had the graph y = 2^x The second graph, y = 1 * 2^ (x3) 4, is a transformation of y = 2^x According to March11, Sal must use PEMDAS to track how y = 2^x will transform He first works with the exponent (E) A 3 was added to the x in y = 2^x, making it y = 2^ (x3) Sal transforms the graph accordingly



Market Value Of Gdp Indicator Of Economic Growth Economic Analysis
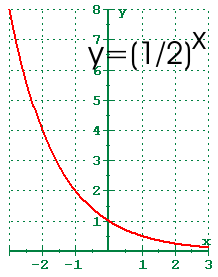


4 1 Exponential Functions And Their Graphs
Press GRAPH to observe the graph of the exponential function along with the line for the specified value of latexf\left(x\right)/latex To find the value of x, we compute the point of intersection Press 2ND then CALC Select "intersect" and press ENTER three timesNote that we also shift the horizontal asymptote in the graph We also show that the point `(0,1)` is translated to `(3,3)` Graph of 'the' Exponential Function amath \begin{example} Graph `y=2^x`, `y=e^x`, and `y=3^x` on the same Cartesian_Coordinatescoordinate plane \end{example} endamathExponential Functions Exponential function exponent contains the variable (x) Graph y = 2x Graph = Definition of Exponential Function An exponential function is a function that can be described by an equation of the form y a b= ⋅ x, where b > 0 and b ≠ 1 Characteristics of an exponential function 1 The function is continuous 2



Exponential Functions Functions Siyavula
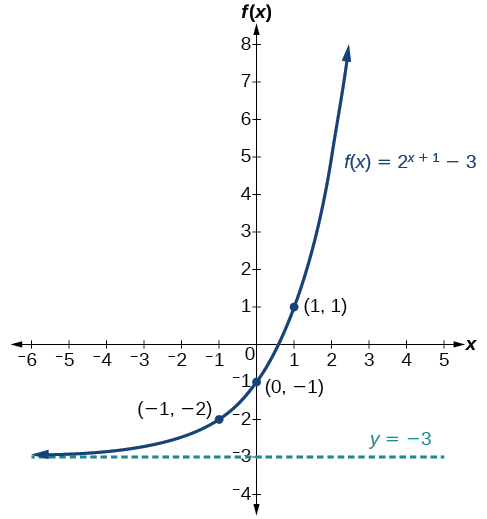


4 2 Graphs Of Exponential Functions Mathematics Libretexts
Finding the equation of an exponential function from the graph Worked example 17 Finding the equation of an exponential function from the graph Use the given graph of \(y = 2 \times 3^{(x p)} q\) to determine the values of \(p\) and \(q\)• The function has a yintercept of 1 Linear, quadratic, and exponential functions can be recognized from their graphs Linear functions are represented by straight lines, quadratic functions by parabolas, and exponential functions by quickly increasing or decreasing curves with a horizontal asymptoteAn exponent indicates the number of times a certain number (the base) is multiplied by itself The exponent, also called the index or power, indicates the number of times the multiplication is repeated For example, \(\text{10}^{3} = 10 \times 10 \times 10 = \text{1 000}\) Graphs of the exponential function \(f(x) = b^{x}\)
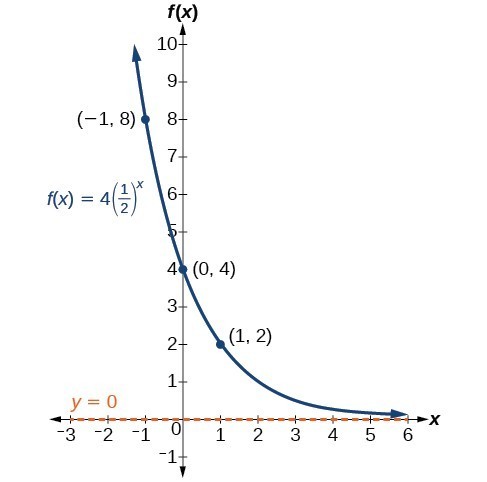


Graph Exponential Functions Using Transformations College Algebra
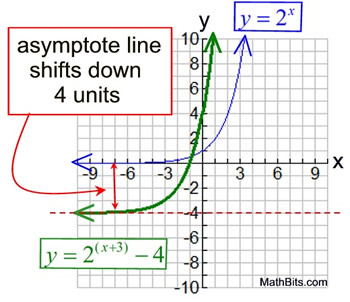


Exponential Functions Mathbitsnotebook Ccss Math
Which graph is represented by the equation y = 2x y = 2x?Replacing y with − y reflects it across the x axis


Intro To Exponential Graphs Expii


Solved Graph The Exponential Function Y 5 2 X Chegg Com


Image The Graphs Of Equation 2 X Equation Equation E X Equation And Equation 3 X Equation


3 1 Exponential Functions And Their Graphs The Exponential Function F With Base A Is Denoted By F X A X And X Is Any Real Number Ppt Download


Hw 4 1 Exponential Functions 1 Definition S Of An Exponential Function Youtube Cute766


Exponential Functions


Logarithmic Functions And Their Graphs


Exponential And Logarithmic Graphs


Exponential And Logarithmic Functions Exponential Functions Sparknotes


Exponential And Logarithmic Graphs


Exponetials And Growth Functions


Solution A Construct A Table Of Values For The Exponential Function Y 2 3 X Use Values Of X From 1 To 3 B Graph The Equation Connect The Points With A Solid Line C What
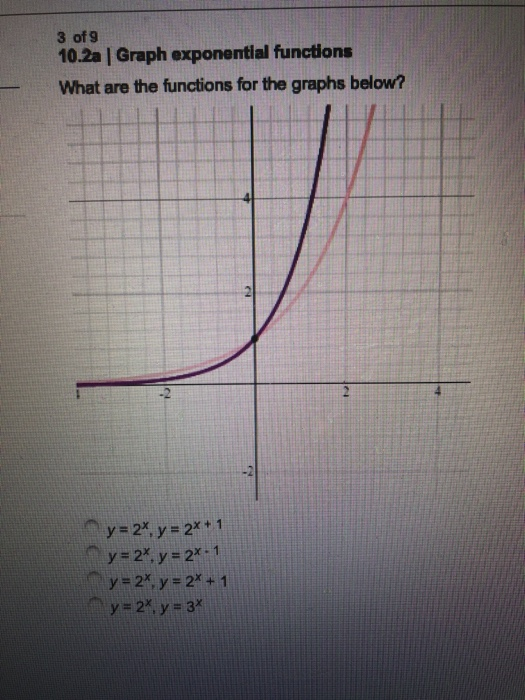


Solved 3 Of 9 10 2a Graph Exponential Functions What Ar Chegg Com


4 2 Graphs Of Exponential Functions Mathematics Libretexts


Exponential Functions



The Exponential Function Math Insight


Logarithmic And Exponential Graphs
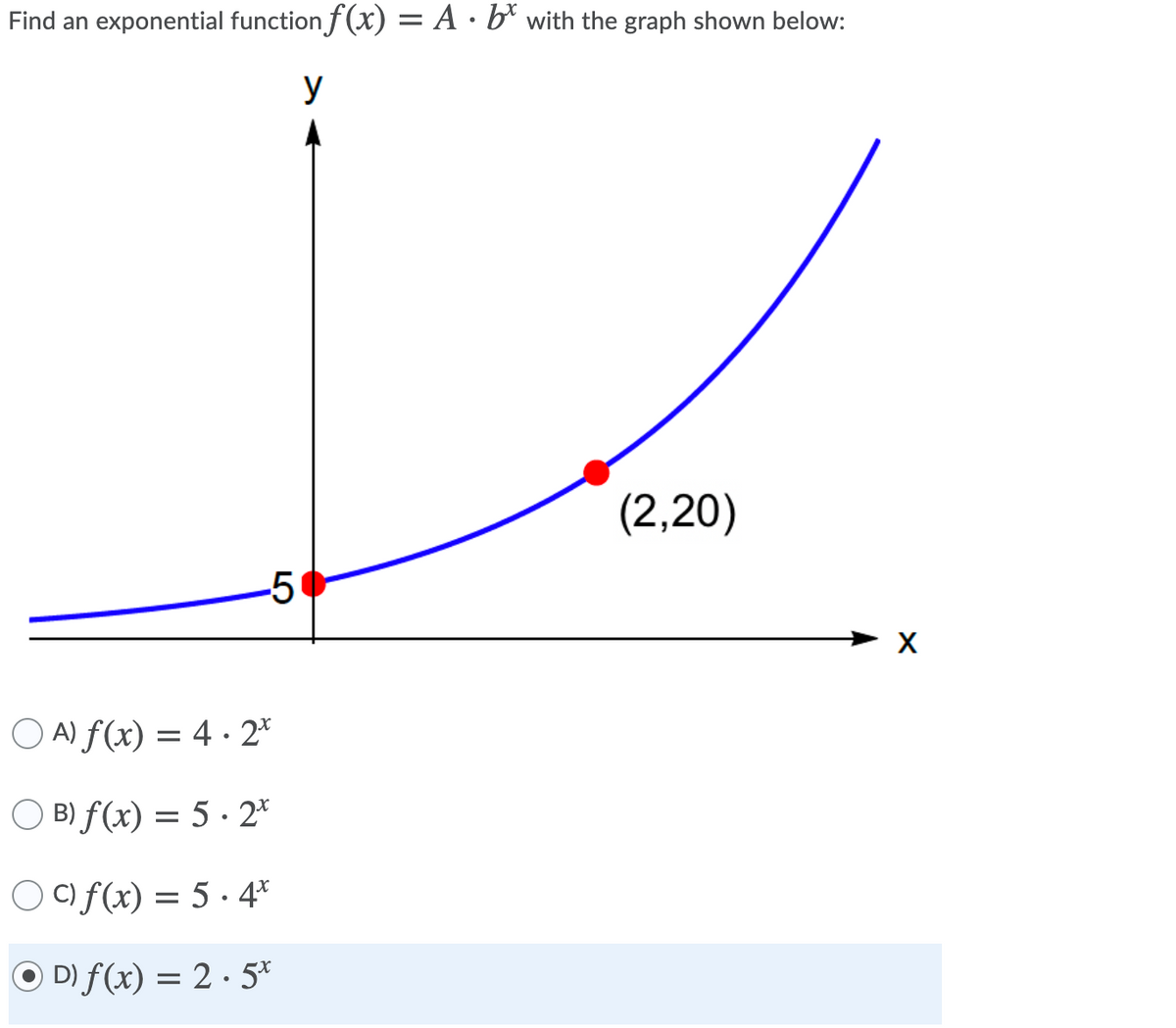


Answered Find An Exponential Function F X A Bartleby


Graphs Of Exponential And Logarithmic Functions Boundless Algebra
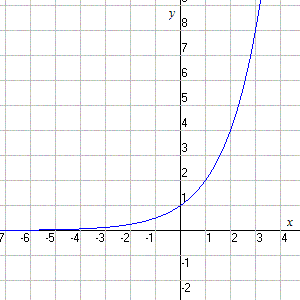


Exponential Functions



Transforming Exponential Graphs Example 2 Video Khan Academy


Graphs Of Exponential Growth Video Khan Academy


Exponential Function Properties Graphs Applications



Graphs Of Exponential Functions Read Algebra Ck 12 Foundation


Graphing Exponential Functions Notes And Practice Flip Ebook Pages 1 8 Anyflip Anyflip
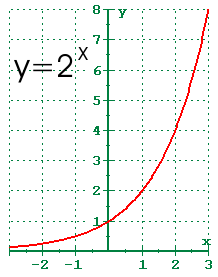


4 1 Exponential Functions And Their Graphs



Graphs Of Exponential Functions


Graphs Solving Equations Exponential Functions Characteristics Transformations 1


Exponential And Logarithmic Functions And Equations Ppt Download


Content How Fast Does An Exponential Function Grow


Lesson 1 Exponential Function And Its Inverse



What Is An Exponential Function Math Class 21 Video Study Com


Exponential Functions And Their Graphs


Solved Y 2 4 5 Graph The Exponential Function Chegg Com


Linear Or Exponential Function
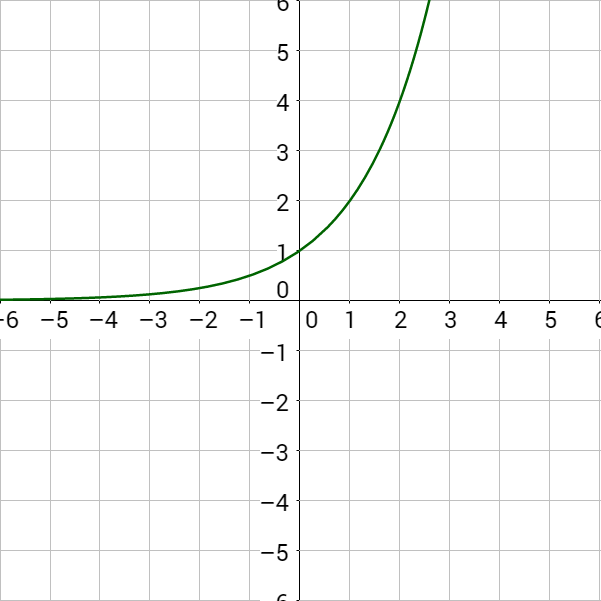


3 01 Exponential Functions
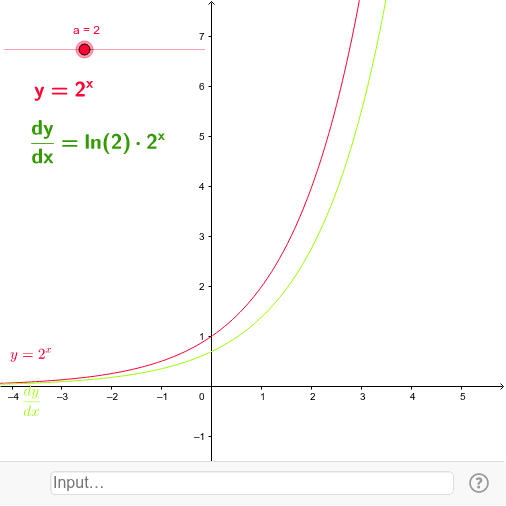


Task 3 Gradient Function Of Exponential Functions Geogebra


Graphing Exponential Functions It Is Important To Know The General Nature And Shape Of Exponential Graphs The Actual Values That May Be Plotted Are Relatively Few And An Understanding Of The General Shape Of A Graph Of Growth Or Decay Can Help Fill In The


Introduction To Exponential Functions
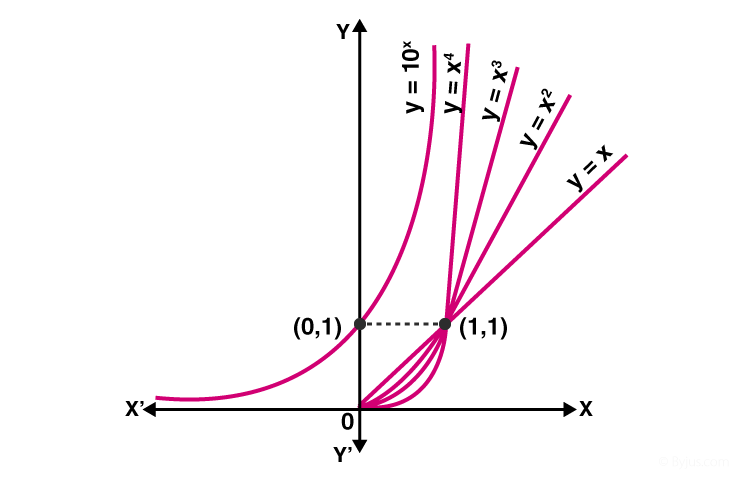


Exponential Functions Definition Formula Properties Rules


Untitled Document
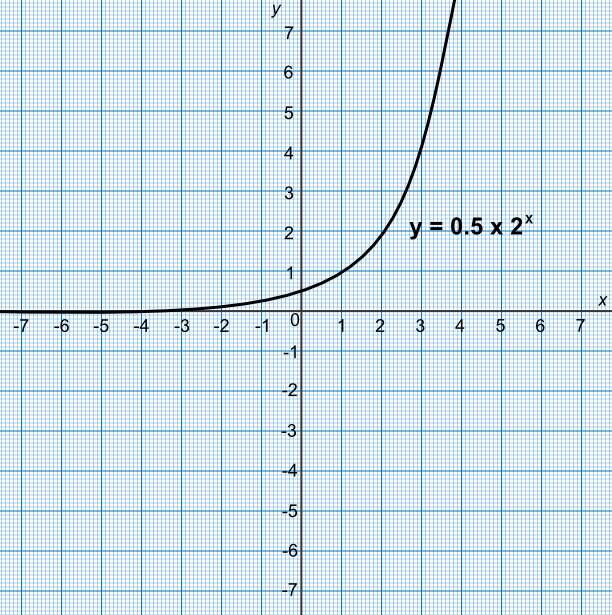


Graphing Exponential Functions


Graphing Exponential Functions Explanation Examples


Graphing Exponential Functions Step By Step Instructions



The Graphs Of The Quadratic Function Y 2x 2and The Exponential Function Y 2 X Are Shown Brainly Com



Can A Function Have More Than Two Horizontal Asymptotes Magoosh Blog High School



Ppt Exponential Functions Powerpoint Presentation Free Download Id



What Is The Graph Of E X Quora


Exponential Functions Mathbitsnotebook Ccss Math


Aim What Is The Exponential Function Do Now Given Y 2 X Fill In The Table X 8 Y Hw Worksheet Ppt Download


Bestmaths



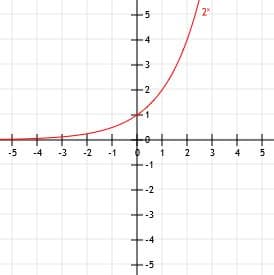
File Exponential Function Y 2 X Svg Wikimedia Commons
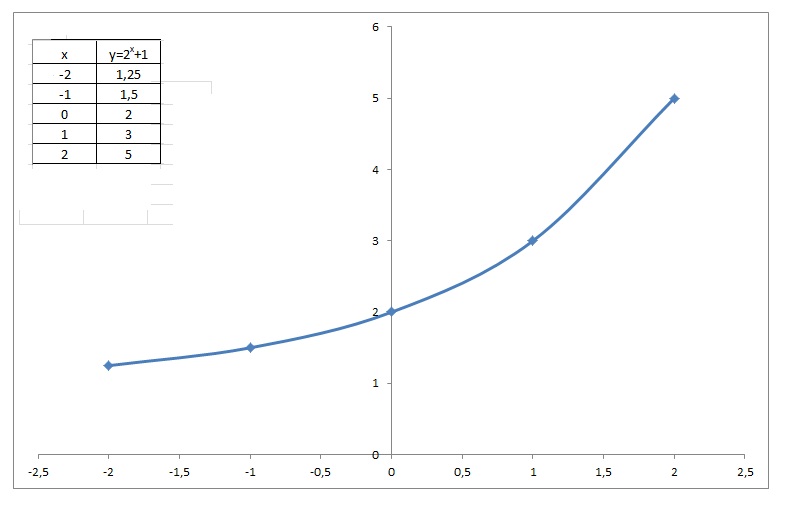


How Do You Graph The Exponential Function Y 2 X 1 Socratic



6 2 Exponential Functions Objectives Classify An Exponential
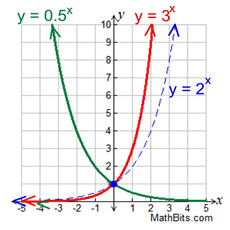


Exponential Functions Mathbitsnotebook A1 Ccss Math
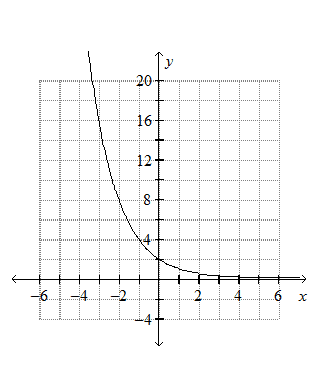


Oneclass Graph The Exponential Function Y 5 2 X



Transforming Exponential Graphs Example 2 Video Khan Academy
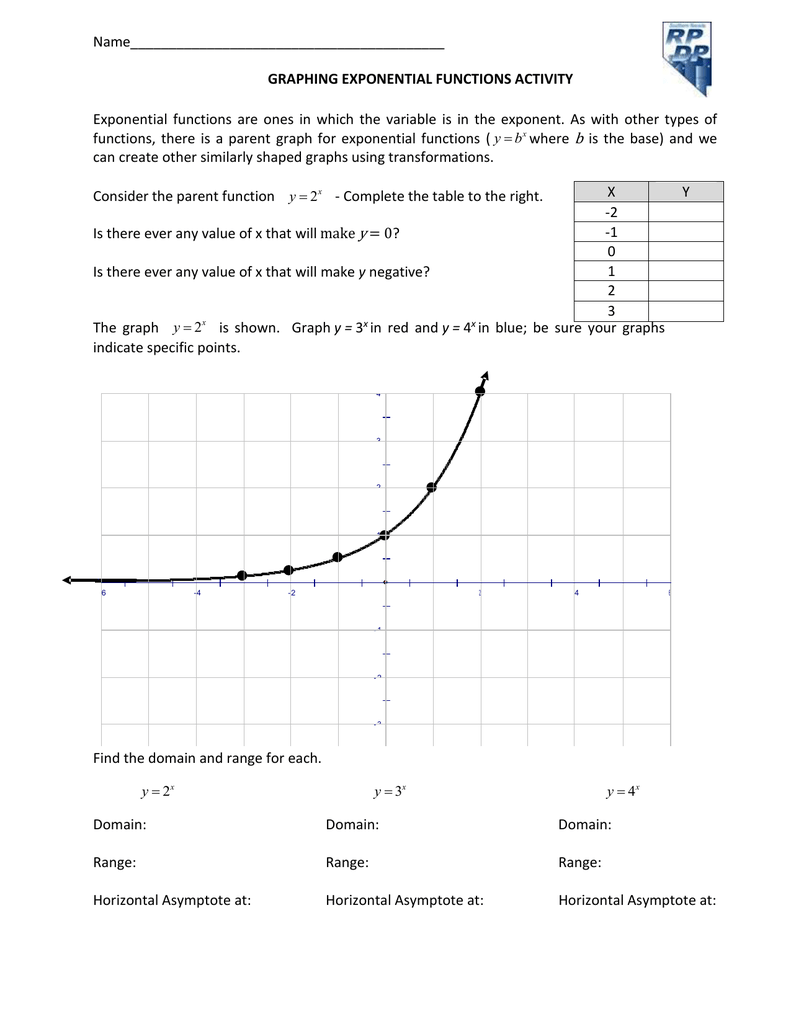


Name Exponential Functions Are Ones In Graphing Exponential Functions Activity


File Exponential Function Y 2 X Svg Wikimedia Commons
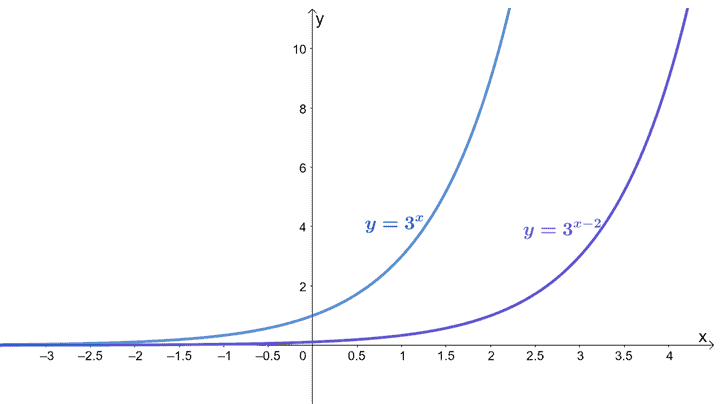


Exponential Function Properties Graphs Applications
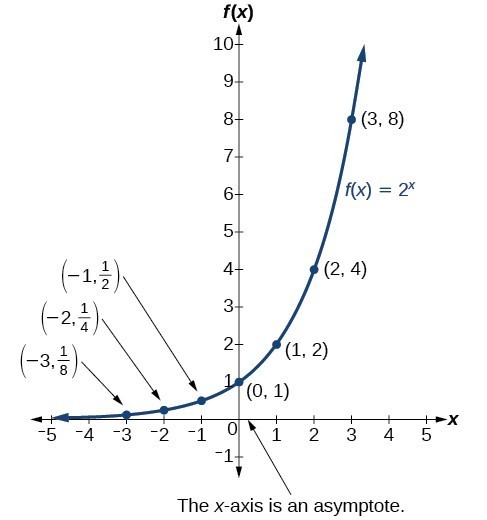


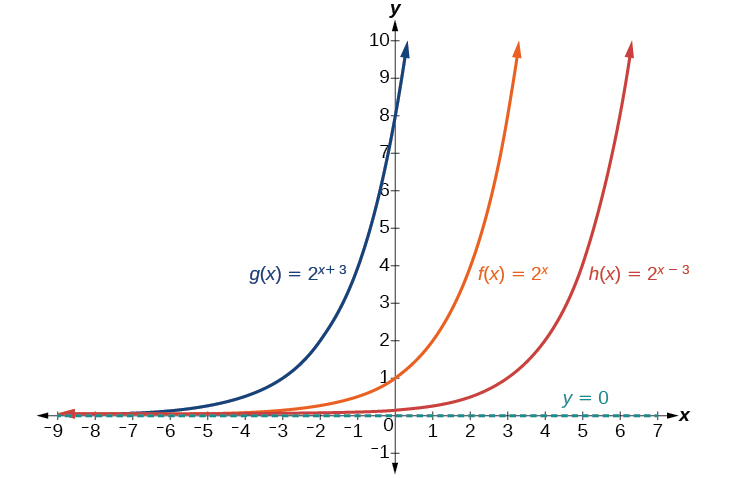
Characteristics Of Graphs Of Exponential Functions College Algebra
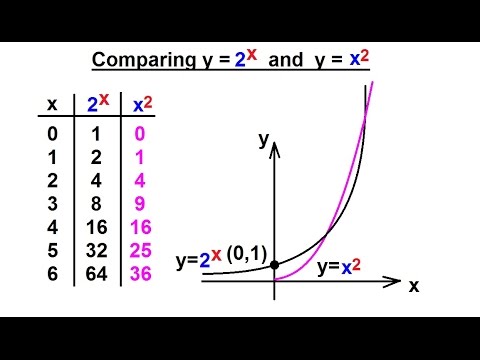


Precalculus Exponential Function 4 Of 13 Comparing Y 2 X And Y X 2 Youtube
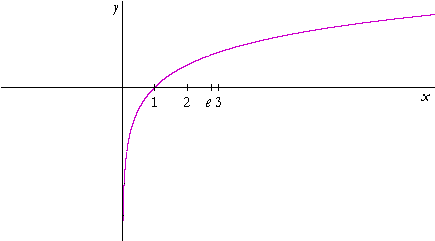


Logarithmic And Exponential Functions Topics In Precalculus



Example 2 Graph An Exponential Function Graph The Function Y 2 X Identify Its Domain And Range Solution Step 1 Make A Table By Choosing A Few Values Ppt Download



Exponential Function Wikipedia


How Do You Graph The Exponential Function Y 2x 1 Class 10 Maths Cbse



0 件のコメント:
コメントを投稿