Solution By the inverse cos formula we know, α = cos1 (Base/Hypotenuse) α = cos1 (√3 /2) Therefore, α = 30°Finding the correct angle from inverse cosine?Click here👆to get an answer to your question ️ Write the value of tan^12sin(2cos^1 √(3)2)

Trigonometric Functions Justin Skycak
Cos inverse 3/2
Cos inverse 3/2-Since z 1 z 2 z 1 = z 1 2 1 2 z 1 2 2 √ 3 2 2 = L e − 1 2 t cos √ 3 2 t 1Let us recall that the principal value of a inverse trigonometric function at a point x is the value of the inverse function at the point x, which lies in the range of principal branch For instance, the principal value of cos−1 (√3/2) is π/6 Since π /6 ∈ 0, π



Evaluate Cos Cos 1 3 2 P 6 Sarthaks Econnect Largest Online Education Community
Cos(7π/6) = √ 3 /2 Multiply our answer by our coefficient of 7 7cos(7π/6) = 7(√ 3 /2) In Microsoft Excel or Google Sheets, you write this function as =7*COS(7PI()/6) Important Angle SummarySine calculator online sin(x) calculator This website uses cookies to improve your experience, analyze traffic and display adsSine, inverse cosine, and inverse tangent 1 Inverse sine function The inverse sine function is written as y = sin−1(x) or y = arcsinx (Not to be confused with y = 1/sinx) The domain of arcsinx is the interval −1,1 and its range is −π 2, π 2 For any number x between −1 and 1, arcsinx is the angle between − π 2 and 2 whose
Welcome to arcsin √(3)/2, our post aboutthe arcsine of √(3)/2 For the inverse trigonometric function of sine √(3)/2 we usually employ the abbreviation arcsin and write it as arcsin √(3)/2 or arcsin(√(3)/2) If you have been looking for what is arcsin √(3)/2, either in degrees or radians, or if you have been wondering about the inverse of sin √(3)/2, then you are rightClick here👆to get an answer to your question ️ Evaluate cos cos^1 (√(3)2) pi6 Join / Login > 12th > Maths > Inverse Trigonometric Functions > Inverse Trigonometric Functions > Evaluate cos cosThe Inverse Sine Function 1 −π π −1 Let's restrict the domain to the interval!
Use the indentity sin (A B) = sin (A)cos (B) cos (A)sin (B) to expand the given expression Use the above indentities to simplify each term in the above expression sin (arccos (1/2)) = √ (1 ( 1/2) 2) = √3/2 (we have used sin (arccos (x)) = √ (1 x 2 )) Substitute and calculateWnte the Value of the Expression Tan ( Sin − 1 X Cos − 1 X 2 ) , When X = √ 3 2 Department of PreUniversity Education, Karnataka PUC Karnataka Science Class 12 Textbook Solutions Important Solutions Inverse Trigonometric Functions (Simplification and Examples) video tutorial ;Thelength of rectangle Then sem twice to theIts breadth andperimeter is 52cm FindLength and breadth




What Is The Value Of Tan 1 2 Cos Inverse 5 3 Quora



Find The Value Of Socratic
Transcript Ex 21, 2 Find the principal value of cos1 (√3/2) Let y = cos1 √3/2 cos y = √3/2 cos y = cos 𝝅/𝟔 ∴ y = 𝝅/𝟔 Since Range of cos1 is 0, 𝜋 Hence, Principal Value is 𝝅/𝟔 (Since cos 𝜋/6 = √3/2)Sin1 x cos1 x = π/2, x ∈ – 1, 1 Inverse Cosine Examples Problem Let the value of the base is √3 and the hypotenuse is 2 Find the value of angle α?By Literature Title Study Guides Infographics by Subject;



How Do You Evaluate Cos 1 1 2 Without A Calculator Socratic




The Value Of Sin 1 3 2 Cos 1 Cos 7pi 6 Is A 5pi
Find the simplified form of cos1 3/5 cos x 4/5 sin x, x ∈ 3π/4,π/4 0 votes 72k views asked in Class XII Maths by nikita74 (1,017 points) Find the simplified form of cos 1 3/5 cos x 4/5 sin x, x ∈ 3π/4,π/4 inverse trigonometric functionsInverse trigonometric functions are widely used in engineering, navigation, physics, and geometry The arccosine of x is defined as the inverse trigonometric function of cosine when 1≤x≤1 When cos y = x Then the arccosine of x is equal to the inverse cosine trigonometric function of x, which is equal to y arccos x = cos1 x = yShare It On Facebook Twitter Email 1 Answer 1 vote answered by Shyam01 (504k points) selected by Chandan01 Best answer = cos π = 1



Evaluate Cos Cos 1 3 2 P 6 Studyrankersonline




The Value Of Cos 1sqrt 2 3 Cos 1 Sqrt6 1 2sqrt3 Is Equa
Inverse cosine calculator Example of Few questions where you can use this formula Find the value of cos−10 c o s − 1 0 in radian Find the value of cos−11 c o s − 1 1 in radian Find the value of cos−125 c o s − 1 25 in ° link to this page by copying the following textCos1 ((√3/2)) = (A) (π/2) (B) (π/3) (π/4) (D) (π/6) Check Answer and Solution for above question from Mathematics in Inverse TrigonometriIf you want to find the answer in a short way,you can use calculatorHere,COS beta =√3/2 Thetefore,Beta=cos^1(√3/2)=30° From this value, Cot Beta=cot30°=√3 Or, cosBeta =√3/2we know that, Sin^2 betacos^2 beta =1 Sin^2 beta=1(√3/2) Sin^2 beta =1/4 Sin beta = 1/2 Therefore, cot beta = (√3/2) ÷(1/2) Cot beta=√3




Example 1 Evaluate Inverse Trigonometric Functions Evaluate The Expression In Both Radians And Degrees A Cos 1 3 2 Solution A When 0 8 P Or 0 180 Ppt Download
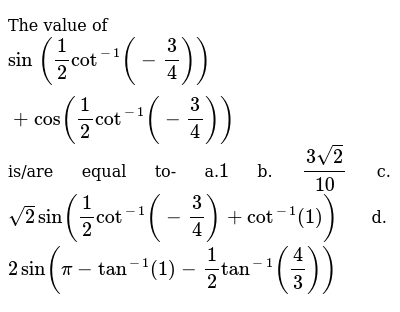



The Value Of Sin 1 2cot 1 3 4 Cos 1 2cot 1 3 4 Is
For such type of problems it is almost always useful to take the angle in the function as say x, ie, take 1/2 cos (inverse) (√5/3) = x That would mean cos (2x) = √5/3 Using cos (2x) = cos^2 (x) 1 cos^2 (x) 1 = √5/3 Solve for cos (x) and then you can get tan (x) which is needed ) 37K views Related Answer2π/3 cot¹ (1) 3π/4 cot¹ (√3) 5π/6 Upgrade to remove ads Only $299/month− π 2, π 2 " Then y =sinx is onetoone Def The inverse sine function is defined by y =sin−1 x if and only if with domain −1,1 and range!



Inverse Sin Negative Square Root 3 Over 2 Youtube




Prove That Sin 1 1 2 Cos 1 Sqrt3 2 Cos 1 1 2 Mathematics And Statistics Shaalaa Com
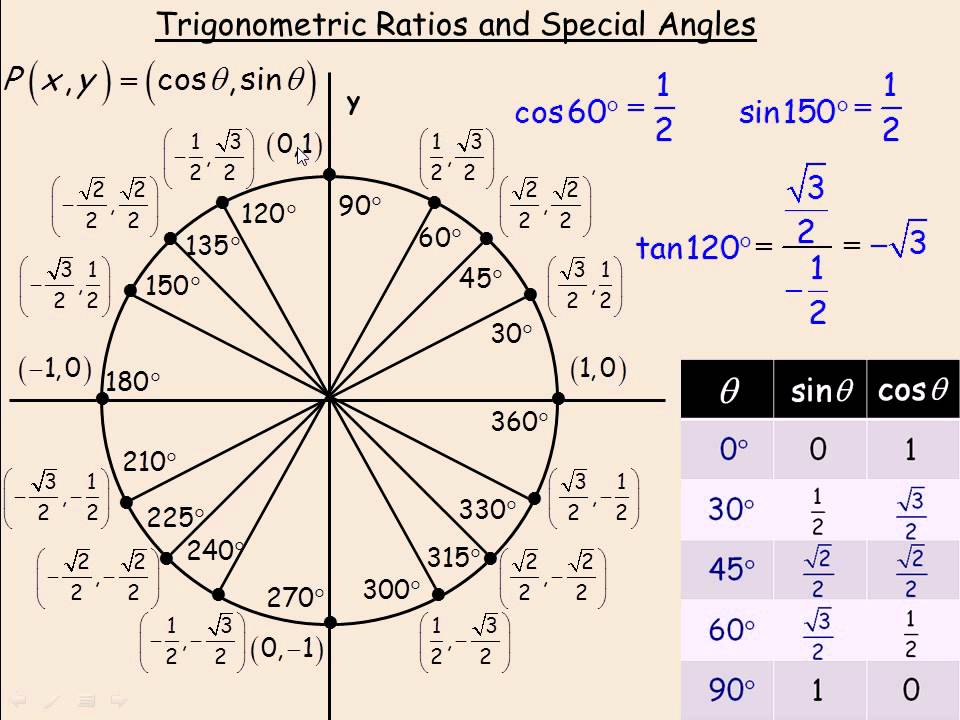
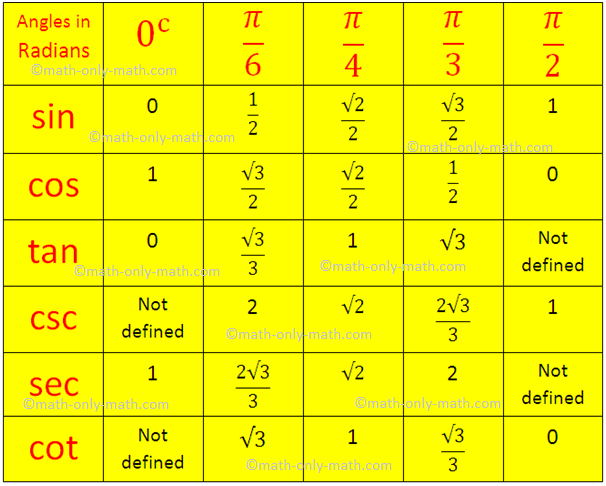
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsThe arccosine of x is defined as the inverse cosine function of x when 1≤x≤1 When the cosine of y is equal to x cos y = x Then the arccosine of x is equal to the inverse cosine function of x, which is equal to y arccos x = cos1 x = y (Here cos1 x means the inverse cosine and does not mean cosine to the power of 1) Example For cos For memorising cos 0°, cos 30°, cos 45°, cos 60° and cos 90° Cos is the opposite of sin We should learn it like cos 0° = sin 90° = 1 cos 30° = sin 60° = √3/2 cos 45° = sin 45° = 1/√2 cos 60° = sin 30° = 1/2 cos 90° = sin 0° = 0 So, for cos, it will be like 1, √3/2




Cos Sin 1 Sqrt 3 2 Find The Exact Value Youtube




Rd Sharma Solutions For Class 12 Maths Chapter 4 Inverse Trigonometric Functions Avail Free Pdf
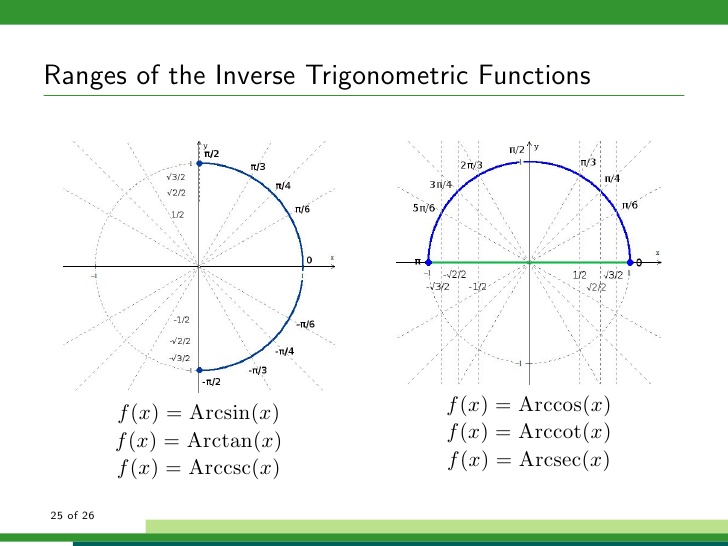
Evaluate coscos1 (√3/2) π/6 inverse trigonometric functions;(ii) cos −1 √3/2 Solution x = cos −1 √3/2 cos x = √3/2 cos x = cos π/6 x = π/6, where x ∊ 0, π (iii) cosec −1 (1) Solution x = cosec −1 (1) Range of cosec1 x is π/2, π/2, so the required angle lies in the above interval cosec x = cosec (π/2) x = π/2, where x ∊ π/2, π/2 (iv) sec −1 (√2)Restrict Cosine Function • The restriction of a cosine function is similar to the restriction of a sine function • The intervals are 0, π because within this interval the graph passes the horizontal line test • Each range goes through once as x moves from 0 to π Inverse Cosine Function • Once we have the restricted function, we are able to proceed with defining the inverse cosine




Example 2 Find Principal Value Of Cot 1 1 Root 3 Examples



How Do You Find The Exact Value Of Arccos 1 Sqrt 2 Socratic
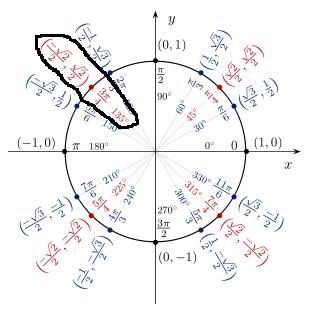
Obj To learn about the inverse sine, inverse cosine, and Evaluate inverse tangent functions 1 sin1( ) 2 sin1( ) 3 sin1( ) 1 2 √3 2 √2 2 1 4 cos1( ) 5 cos1( 1 ) 6 cos1( ) 1 27 tan1 ( 0 ) 8 tan1 ( 1 ) 9 tan1 ( √ 3 )Example 231 Find the inverse Laplace transforms of a e 2 z z 2 b 8 e 3 z z 2 4 from ME 111 at UET Peshawar Study Resources Main Menu;Inverse cosine calculator cos1 150° 5π/6√ 3 /2 135° 3π/4√ 2 /2 1° 2π/31/2 90° π/2 0 60° π/3 1/2 45° π/4 √ 2 /2 30° π/6 √ 3 /2 0°




How Do You Use Inverse Trigonometric Functions To Find The Solutions Of The Equation That Are In The Interval 0 2p Socratic




Sin Pi 6 Cos 1 Sqrt 3 2 Youtube
C Trig Functions of Any Angle The definitions based on an acute angle in a right triangle extend to trig functions of any angle r is always >0, so signs of functions in any quadrant pop right out from signs of x and y in that quadrant Do quadrant angles by reference to x y r, eg cos 0° = 1/1 = 1 and sin π = 0/−1 = 0Cot Inverse Calculator Are you looking for a smart tool that calculates the cotangent inverse of a real number or fraction within no time?Then, you have arrived the correct place and our calculator is the best tool that you are looking for The main aim of our Cot Inverse Calculator is to calculate the cotangent inverse of numbers simply and quicklyInverse trigonometric ratios are the inverse of the trigonometric functions operating on the ratio of the sides of the triangle to find out the measure of the angles of the rightangled triangle The inverse of a function is denoted by the superscript "1" of the given trigonometric function For example, the inverse of the cosine function will be cos1
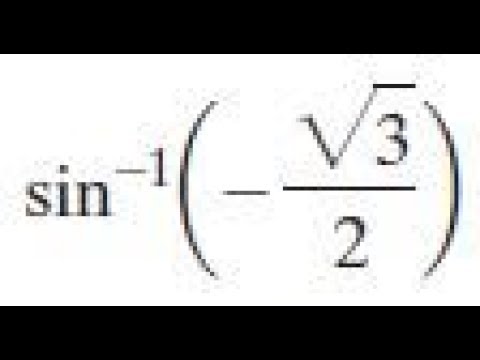



Sin 1 Sqrt 3 2 Find The Exact Value Of Each Expression Youtube




Tan 1 2 Cos 1 5 3 Brainly In
3) √3/2 4) 1/√2 Answer (2) 1/2 Solution Given, 4 sin1 (x) cos1 (x) = π 3 sin1 (x) sin1 (x) cos1 (x) = π 3 sin1 (x) (π/2) = π 3 sin1 (x) = π – (π/2) 3Cosine rule can be used for any triangle (whether it is rightangled triangle or not) to relate all the side of the triangle to one angle Rule for finding sides a 2 = b 2 c 2 2bc * cos (A) b 2 = a 2 c 2 2ac * cos (B) c 2 = a 2 b 2 2ab * cos Rule for finding angles cos (A) = b 2 c 2 a 2 / 2bcInsure the inverse is a function Mark the axes that represent the angle measure 7 We use the names sin1, cos1, and tan1 or Arcsin, Arccos, and Arctan to represent the inverse of these functions on the limited domains you explored above The values in the limited domains of sine, cosine and tangent are called principal values (Similar to



Evaluate Cos Cos 1 3 2 P 6 Sarthaks Econnect Largest Online Education Community




A Determine The Value Of8 1 Sin 8 1 2 6 Gauthmath
− π 2, π 2 " NOTE The inverse sine function is also called arcsine,denotedbyy =arcsinx L30 2 34thIn trigonometrical ratios of angles (180° θ) we will find the relation between all six trigonometrical ratios We know that, sin (90° θ) = cos θ cos (90° θ) = sin θ tan (90° θ) =Ask Question Asked 7 years, 5 months ago Active 7 years, 5 months ago Viewed 44 times 1 For my math homework, I have to find an angle of rotation, θ, by cos θ = − 3 / 2 When I plug this into my calculator, I get 5 π /6, but the correct answer is 5 π /6




Evaluvate Cos Cos Inverse Square Root 3 2 Pi 6 Maths Inverse Trigonometric Functions Meritnation Com



Find The Value Of Sin 2tan 1 2 3 Cos Tan 1 3 Sarthaks Econnect Largest Online Education Community
4 Let P = a i j be a 3 × 3 matrix and let Q = b i j where b i j = 2 i j a i j for 1 ≤ i, j ≤ If the determinant of P is 2, then the determinant of the matrix Q is 5 If the sum of n terms of an AP is given by S n = n 2 n, then the common difference of the AP is 6 Prove sin(inverse)(1/2) cos(inverse)(√3/2)= 2 /3 Maths Inverse Trigonometric FunctionsQuestions Show answers Question 1 SURVEY 300 seconds Report an issue Q sin 1 (1/2) answer choices π/3



Find The Values Of Tan 1 1 Cos 1 1 2 Sin 1 1 2 Sarthaks Econnect Largest Online Education Community




Misc 12 Chapter 2 Inverse Trigonometry Prove 9pi 8 9 4
answeredby rubby(5kpoints) selectedby Vikash Kumar Best answer The principal value of cos1(√3/2) is 5π/6 Please log inor registerto add a comment 1vote answeredby Nandy(50points) X=coc^1(√3/2)=πcos^1(√3/2) =ππ/6=5π/6Tan 1 (√3) π/3 OTHER SETS BY THIS CREATOR Inverse Trig Graphs 6 terms chuc_an_tran Inverse Trigonometry Functions Domain and Range 12 terms chuc_an_tranWhat are the relations among all the trigonometrical ratios of (180° θ)?



How To Find The Value Of Tan 1 2 Cos 1 5 3 Quora




The Value Of Sin 1 Sqrt 3 2 Is A Pi 3 B
Evaluate cos cos1 (√3/2)π/6 0 votes 150k views asked in Class XII Maths by nikita74 (1,017 points) inverse trigonometric functions AB = cos inverse of √3/2 AB = π/6 ABAB = π/2 π/6 2A = 4π/6 ⇒A = π/3 ABAB = π/2 π/6 2B = π/3 ⇒B = π/6 there are 4 sets of answers New questions in Math X^2/(xsinx5cosx)^2 Hw& Question 9 cos1 (1/√2) Solution Let cos1 (1/√2) = y then, cos y = 1/√2 Range of principal value for cos1 is 0, π and cos(2π/3) = 1/2 Therefore, principal value of cos1 (1/2) = 3π/4 Question 10 cosec1 (√2) Solution Let cosec1 (√2) = y then, cosec y = √2




For The Principal Values Evaluate Each Of The Following Sin



Www3 Nd Edu Apilking Calculus2resources Lecture 6 Slidesl6 Pdf
Once again, this may involve the use of the "2nd" key to obtain cos−1 cos−1 (0343) = 1269 ≈ 1221 5/7 57 Inverse Trigonometric Functions PRACTICE TEST Question 9 Grade 10 / 10 Find the exact value of the inverse sine, cosine, and tangent of − −1 sin (– √ – √3 3 = ) 2 , if possible 2 – − π (33%) 3 −1 cos (– 5 π √ – 3 = ) 2 (33%) 6 −1 tan (– √ – 3 = ) 2 The exact valueCos (2π/3) = 1/2 Principal Value of Inverse Trigonometric Functions When there are two values, one is positive and the other is negative such that they are numerically equal, then the principal value of the inverse trigonometric function is the positive one For instance, the principal value of cos − 1 (√3/2
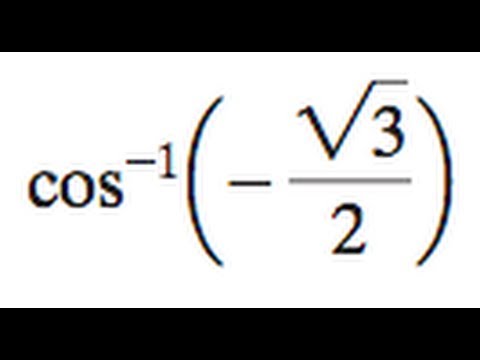



Inverse Cos Sqrt 3 2 Youtube




Provethat Cos Sin 1 3 5 Cot 1 3 2 6 5 Root 13 Brainly In
Q cos1 (√3/2) = answer choices π/3 2π/3 π/6 5π/6 s Question 4 SURVEY 60 seconds Q What range of angles can you get from inverse cosine?



Prove The Following Cos Sin 1 3 5 Cot 1 3 2 6 5 13 Sarthaks Econnect Largest Online Education Community




Exact Value Of Sin Cos 1 1 2 Sin 1 3 5 Trigonometric Inverse Compound Angle Youtube




Example Find Solution Of Sin X Root 3 2 Class 11




The Value Of Sin 1 Cos Sin 1 Sqrt 3 2 Is




How Do You Evaluate Cos 1 Sqrt3 2 Socratic




If 4 Cos 2theta Sqrt 3 2 Sqrt 3 1 Costheta Then Theta Is




Exact Vluea Of Sin Sin 1 3 5 Cos 1 4 5 Inverse Trigonometric Ratio Negative Value Youtube




Write The Value Of Tan 1 2sin 2cos 1 3 2




Cos Cos 1 Root3 2 Pi 4 Maths Inverse Trigonometric Functions Meritnation Com




Sin 1 X Cos 1 X Pi 6 Brainly In




Show That Cos 1 Cosalpha Cosbeta1 Cosalphacosbeta 2tan 1 Tan Alpha2tan Beta2




Trigonometric Functions Justin Skycak



Prove That Sin 1 Cot Sin 1 2 3 4 Cos 1 12 4 Sec 1 2 0 Sarthaks Econnect Largest Online Education Community




Cos Cos 1 Sqrt 3 2 Pi 6 Youtube



1




Solving Trig Equation Of Cos X 3 2 Youtube




Prove Cos 1 X Cos 1 X 2 Root 3 3x 2 2 Pi 3 Teachoo




Prove That Sin 1 1 2 Cos 1 Sqrt3 2 Cos 1 1 2 Mathematics And Statistics Shaalaa Com




If Cos Theta Sqrt 3 2 And Theta Lies In Quadrant Iii Find The Values Of All The Youtube




Cos 1 Sqrt 3 2 Find The Exact Value Of Each Expression Youtube
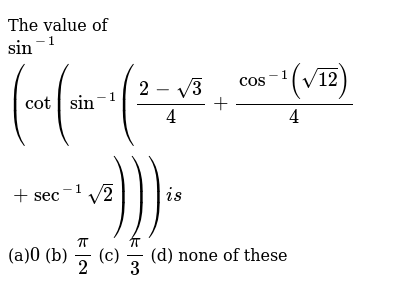



The Value Of Sin 1 Cot Sin 1 2 Sqrt 3 4 Cos 1 Sq




Ex 2 1 14 Find Value Of Tan 1 Root 3 Sec 1 2 Ex 2 1




Sin 1 How To Derive Sin 1 Degrees Value




Taking Only Principal Values The Values Of Cos 1 1 2 Sin




Ncert Exemplar Solutions For Class 12 Maths Chapter 2 Inverse Trigonometric Functions Access Free Pdf




Find The Principal Value Of I Sin 1 1 Sqrt 2
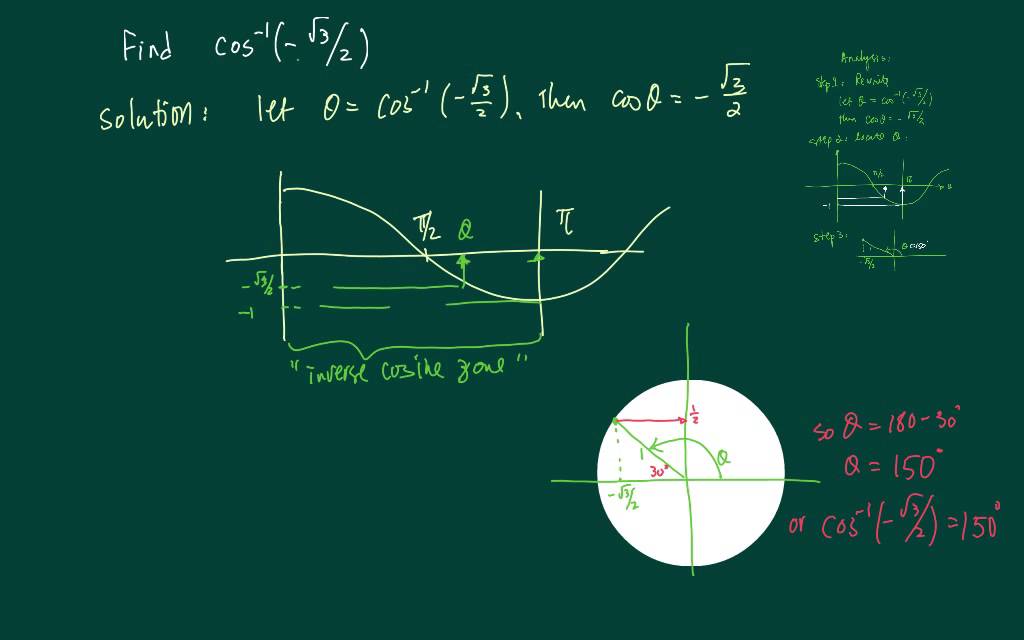



How To Work With Arccosine Inverse Cosine Arccos Sqrt 3 2 Youtube




Example Find Solution Of Sin X Root 3 2 Class 11



Write The Value Of Tan 1 2sin 2cos 1 3 2 Sarthaks Econnect Largest Online Education Community




Find The Value Of Sin 1 Cos Sin 1 Sqrt 3 2



Derivatives Of Inverse Trigonometric Functions
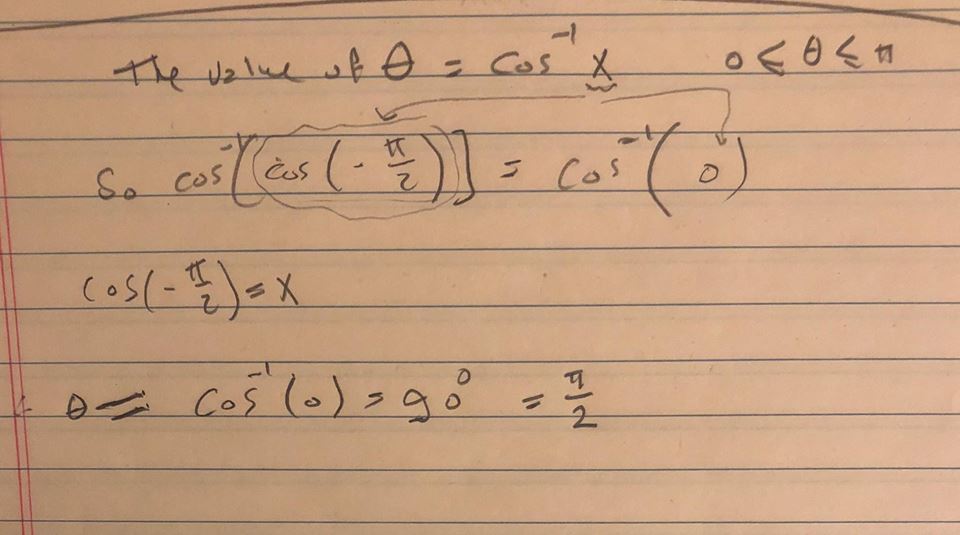



How Do You Evaluate Cos 1 Cos Pi 2 Socratic




Solve Sin Cos 1 3 5 Cot 1 5 12 Youtube



Http Www Math Utah Edu Anna Fall12 Lessonplans Section68 Pdf




75 Square Root Digiphotomasters




Please Explain In Details How The 3 The Square Chegg Com




Evaluate That Cos Cos 1 Sqrt 3 2 Pi 6



Prove The Following Cos Sin 1 3 5 Cot 1 3 2 6 5 13 Sarthaks Econnect Largest Online Education Community
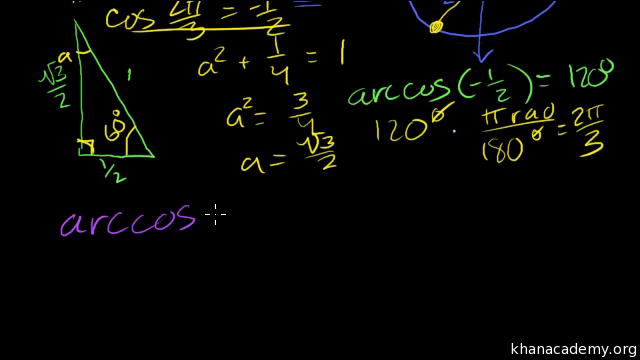



Intro To Arccosine Video Trigonometry Khan Academy




Ex 2 2 Find Sin Pi 3 Sin 1 1 2 Class 12 Ncert
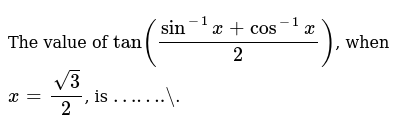



The Value Of Tan Sin 1 X Cos 1 X 2 When X Sqrt 3




If Sin Theta 1 2 And Cos Theta Root 3 2 Then Find The Value Of Tan Theta Tan Theta 1 Minus Tan Brainly In




Prove That Cos 1 X 2 Sin 1 Sqrt 1 X 2 2 Cos 1 Sqrt 1 X 2 Youtube




Ex 2 1 2 Find Principal Value Of Cos 1 Root 3 2 Class 12



Trigonometric Functions Of Any Angle Trigonometry Socratic




How Does Cos 1 1 2 2pi 3 Study Com



If Y Cos 1 2x 3 1 X 2 13 Then Find Dy Dx Sarthaks Econnect Largest Online Education Community



Prove That Cos 1 X Cos 1 X 2 3 3x 2 2 P 3 Sarthaks Econnect Largest Online Education Community




The Value Of Sin 2 Cos 1 1 2 Cos 2 Sin 1 1 3 Is




Prove Cos 1 X Cos 1 X 2 Root 3 3x 2 2 Pi 3 Teachoo




Ex 2 2 18 Tan Sin 1 3 5 Cot 1 3 2 Class 12 Ncert




Cos Sin 1 Sqrt 2 3 Youtube



What Is The Value Of Sin 3 2 Quora




Find The Value Of Sin 1 Sqrt 3 2




Finding The Inverse Sine Of Radical Three Over Two Youtube




Evaluate Tan 1 3 Sec 1 2



Trigonometrical Ratios Table Trigonometric Standard Angles Standard



Q Tbn And9gcswsf Ecpsduz38bfjvi Leyscrwp8sy42we07iguooyebhgdbn Usqp Cau



What Will Be The Value Of Sin Inverse Root3 2 Quora



1



What Is The Sin 1 Sqrt 3 2 Socratic




Cos Cos 1 3 2 Pi 4 Maths Inverse Trigonometric Functions Meritnation Com




The Value Of Cos Cos 1 3 2 P 6 Is Brainly In



Evaluate Sin 2 Cos 1 3 5 Sarthaks Econnect Largest Online Education Community




Tan Cos 1 Sqrt 3 2 Youtube



What Is The Value Of Cot Cosec Inverse 5 3 Tan Inverse 2 3 Quora
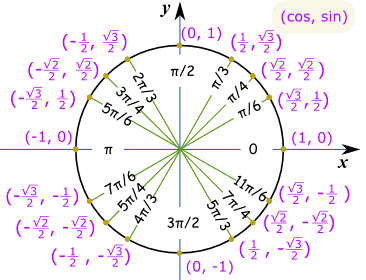



Unit Circle




Write The Value Of Sin 1 Sqrt 3 2 Cos 1 1 2



What Is The Principal Value Of Cos 1 3 2 Sarthaks Econnect Largest Online Education Community
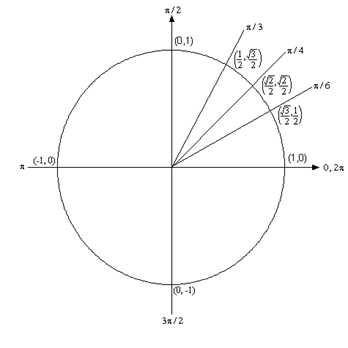



Algebra Trig Review



Q Tbn And9gcswsf Ecpsduz38bfjvi Leyscrwp8sy42we07iguooyebhgdbn Usqp Cau




Sin 1 Circ Is Irrational But How Do I Prove It In A Slick Way And Tan 1 Circ Is Mathematics Stack Exchange




Sin Pi 3 Sin 1 Sqrt 3 2



How To Find The Value Of Tan 1 2 Cos 1 5 3 Quora



0 件のコメント:
コメントを投稿